Scala

Introduction to Recursion Schemes with Matryoshka

Anatolii

Mar 10, 2017 — 14 min read

Recursion is the GOTO of functional programming - Erik Meijer^1

Recursive data structures

In our daily programming life, we encounter recursive data structures on a regular basis. The best-known examples include linked lists and trees. Often working with such data structures we have a need to evaluate (collapse) them to a value. For example:

Given a list of integers, say 1, 2 and 3, one may want to find their sum 6.
Given a parser of arithmetic expressions, such as 2 * 3 + 3, we can expect it to produce a tree out of that expression - Add(Mult(Num(2), Num(3)), Num(3)). Such trees often need to be evaluated by actually performing these mathematical operations.
A more abstract example: natural numbers. Given the number zero and an ability to construct a successor of any natural number, you can construct all the natural numbers. If Zero is such a zero number, and Succ(x) constructs a natural number following x, Succ(Succ(Succ(Zero))) can represent 3. This is also a recursive structure, and the simplest operation you want to do on it is to actually evaluate it to an Int: Nat => Int.

In this article, we shall see how all of these examples involve recursion. Don't Repeat Yourself (DRY) is one of the fundamental principles of programming - so, if we repeat recursion from example to example, we should abstract it away. We shall see how to do that.

But first, let us set the foundation by doing all of the above examples in code.

Natural Numbers

Here is how an implementation of natural numbers might look like:

// Nat
sealed trait Nat
case class   Succ(previous: Nat) extends Nat
case object  Zero                extends Nat

And here is a visualization of the number 3 represented this way:

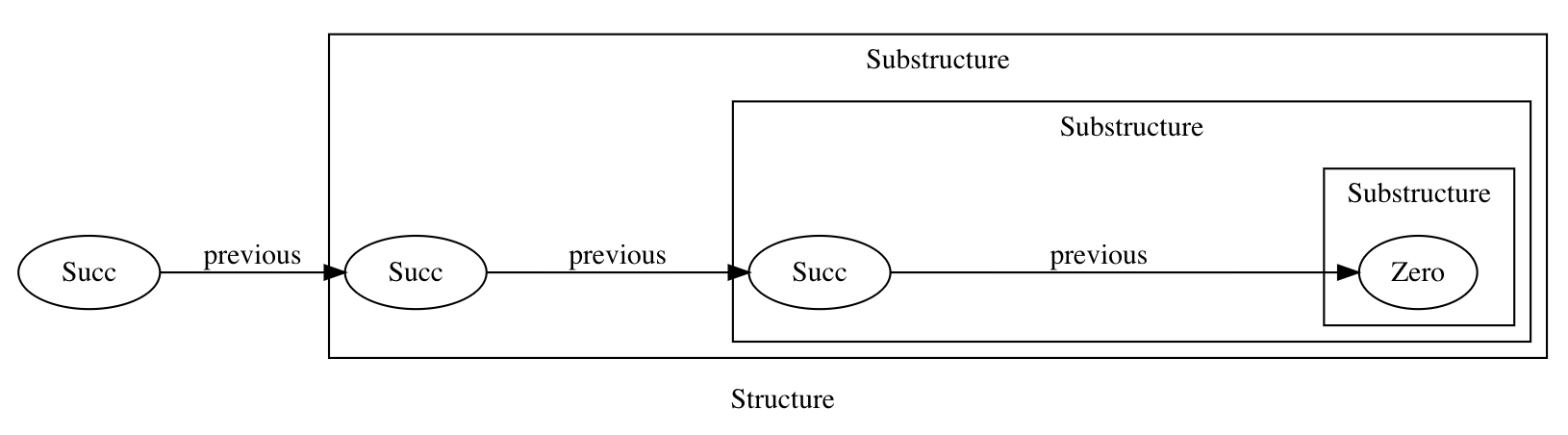
This would correspond to Succ(Succ(Succ(Zero))). Note the recursive nature of this structure: a smaller substructure of the same type is present in every structure (except the terminal one, Zero).

Now, let us see how to evaluate a natural number to an Int. In order to do this for an arbitrary Succ(x), we need to evaluate x and add 1 to the result. Zero should evaluate to 0:

// Nat to Int
def natToInt(n: Nat): Int = n match {
  case Succ(x) => 1 + natToInt(x)
  case Zero    => 0
}
val nat = Succ(Succ(Succ(Zero)))
val natRes: Int = natToInt(nat)
println(natRes)  // 3

Lists

Now let us see how to implement a list as a recursive structure:

// List
sealed trait IntList
case class   Cons(head: Int, tail: IntList) extends IntList
case object  Empty                          extends IntList

A list is either an empty list or a recursive structure that has a head element and a tail - a sublist representing all the elements following the head. For simplicity, we only consider lists of Int.

Here is how a list of 1, 2, 3 looks like:

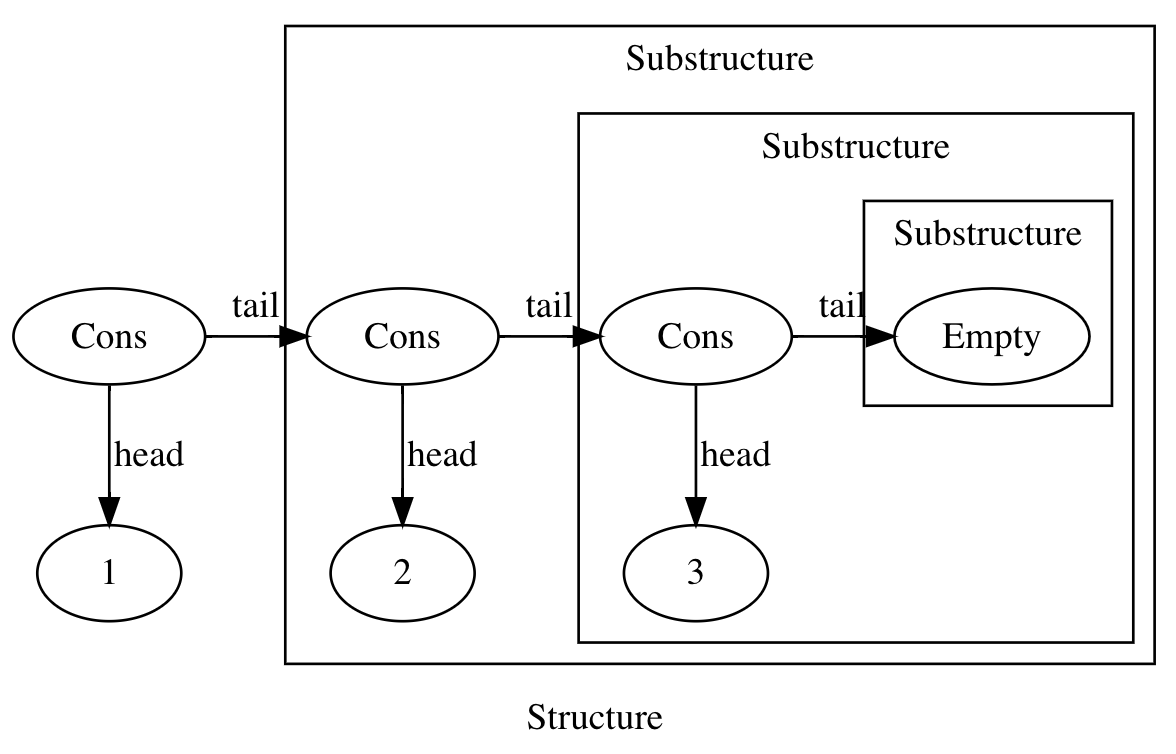
In order to find the sum of all the elements in a list, we should add its head to the sum of all the elements of its tail. If the list is Empty, the result of the summation is 0:

// Sum a list of ints
def sumList(l: IntList): Int = l match {
  case Cons(head, tail) => head + sumList(tail)
  case Empty            => 0
}
val lst = Cons(1, Cons(2, Cons(3, Empty)))
val listRes: Int = sumList(lst)
println(listRes)  // 6

Expressions

Finally, this is a definition of a tree aiming to represent mathematical expression:

// Expr
sealed trait Expr
case class   Add (expr1  : Expr, expr2: Expr) extends Expr
case class   Mult(expr1  : Expr, expr2: Expr) extends Expr
case class   Num (literal: Int              ) extends Expr

We have two node types for the summation and the multiplication, and one leaf type for the numbers.

Here is how an expression 2 * 3 + 3 looks like:

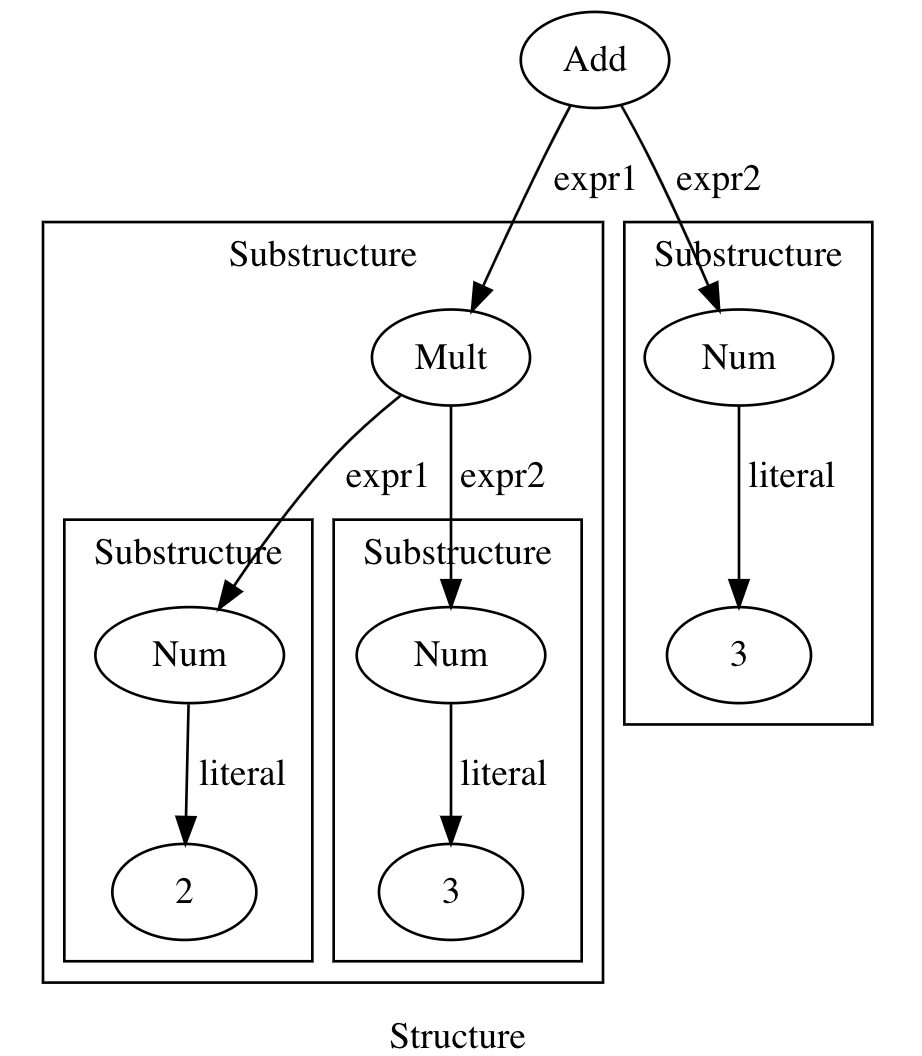
How do we evaluate it? If it is a node representing a mathematical operation, first we need to evaluate its children and then do an operation represented by this node. If it is a leaf - a number - it just evaluates that number:

// Evaluate an expression
def eval(e: Expr): Int = e match {
  case Add (x1, x2) => eval(x1) + eval(x2)
  case Mult(x1, x2) => eval(x1) * eval(x2)
  case Num (x)      => x
}
val expr = Add(Mult(Num(2), Num(3)), Num(3))
val exprRes: Int = eval(expr)
println(exprRes)  // 9

Generalisation

Structure preserving transformations

Intuitively, every example above is similar. All of them involve a recursive structure that is collapsed from the "bottom" (the terminal element with no child substructures) to the "top" (the root structure). What is in common between the natToInt, sumList and eval functions? Can we abstract away these common elements, so that every one of these functions can be expressed in the same terms?

Every example works on a recursive structure - a structure that has substructures of the same type as parts of itself.
They all involve recursive calls in order to transform these substructures. So, natToInt is called recursively on previous in order to evaluate Succ(previous).
The results of these transformations are combined according to the parent structure.
- In sumList(Cons(head, tail)), head is a part of the parent structure. tail is a substructure that is evaluated recursively via sumList(tail) and then combined with that head via addition.
- In eval of either Add or Mult, we first need to call eval on the child expressions of these nodes, and then combine them depending on the parent structure - if it is Add, we do addition, if Mult - multiplication.

A better way to look at it is as if we were replacing the substructures by their evaluations and then evaluating the resulting structure.

For example, when evaluating a Nat depicted by the diagram above, the next step of its evaluation would look as follows:

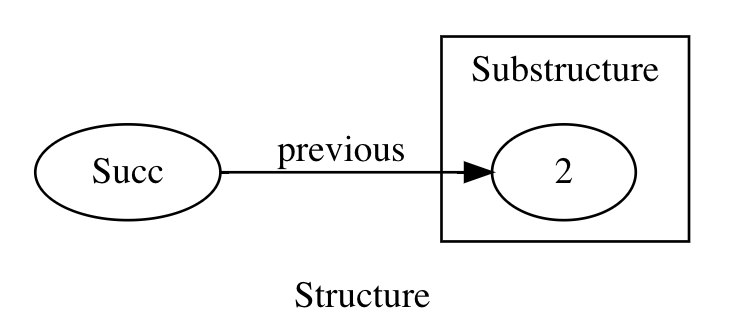
Effectively, we have Succ(previous = 2), which is then collapsed into 1 + 2 == 3. However, previous is supposed to be a Nat, not an Int. In order to be able to write the above statement, we can allow the substructure to have an arbitrary type: Succ[A](previous: A).

Similarly, the next step for the IntList depicted above will be:

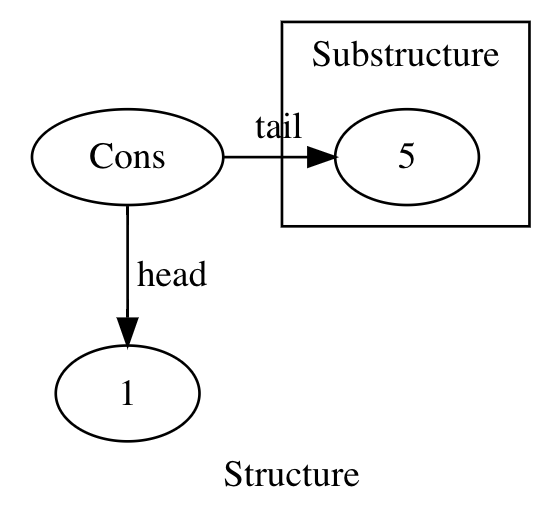
This is effectively a Cons[Int](head = 1, tail = 5) (again, notice how we introduce a type parameter for the substructure). After that, the head is added to the new tail, resulting in 6

Finally, for the Expr above, the next step is to evaluate both of its two substructures:

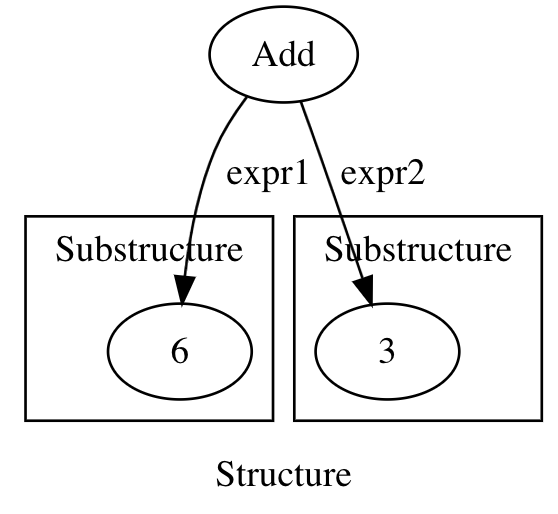
This is an Add[Int](expr1 = 6, expr2 = 3), and the next step is to collapse it by doing 6 + 3.

We are dealing with a structure-preserving transformation here. These kind of transformations are well understood in terms of functors.

If we redefine our recursive structures such that they are parameterized by the type of their substructure, their types will have a form F[A] and we will be able to define functor instances for them.

Ordinarily, A in these F[A] is another F[_] (a substructure, reflecting the recursive nature of the parent structure) or Nothing (for terminal elements that do not have substructures). In our examples, we first do a map, turning F[A] into F[B], where B is the type we are evaluating the structure into (in all our examples, B is Int). Next, given F[B], we collapse it into a B. A function F[B] => B is called an Algebra (Matryoshka definition, https://en.wikipedia.org/wiki/F-algebra).

Now let us see how this theory can be applied in practice.

New definitions for the recursive structures

In all our data structures, we need to specify the type of the substructures as a type parameter, so that we can then evaluate these substructures in a way that preserves the parent structure, via map.

The new definitions can go as follows:

// Nat
sealed trait Nat [+A]
case class   Succ[ A](previous: A) extends Nat[A      ]
case object  Zero                  extends Nat[Nothing]

// List
sealed trait IntList[+A]
case class   Cons   [ A](head: Int, tail: A) extends IntList[A]
case object  Empty extends IntList[Nothing]

// Expr
sealed trait Expr[+A]
case class   Add [ A](expr1  : A, expr2: A) extends Expr[A      ]
case class   Mult[ A](expr1  : A, expr2: A) extends Expr[A      ]
case class   Num     (literal: Int        ) extends Expr[Nothing]

Functors

If we want to use map on these data structures, they need functor instances. The definitions below are straightforward (do not forget to import scalaz._, Scalaz._, which is needed to bring functors in scope):

// Functors
implicit val natFunct: Functor[Nat] = new Functor[Nat] {
  def map[A, B](fa: Nat[A])(f: A => B): Nat[B] = fa match {
    case Succ(x) => Succ(f(x))
    case Zero    => Zero
  }
}

implicit val intListFunct: Functor[IntList] = new Functor[IntList] {
  def map[A, B](fa: IntList[A])(f: A => B): IntList[B] = fa match {
    case Cons(head, tail) => Cons(head, f(tail))
    case Empty            => Empty
  }
}

implicit val exprFunct: Functor[Expr] = new Functor[Expr] {
  def map[A, B](fa: Expr[A])(f: A => B): Expr[B] = fa match {
    case     Add (x1, x2) => Add (f(x1), f(x2))
    case     Mult(x1, x2) => Mult(f(x1), f(x2))
    case x @ Num (_     ) => x
  }
}

Catamorphism: first attempt

As discussed above, all we need to collapse a recursive structure is to map its substructures by the collapse function and then evaluate the resulting structure via an algebra. This recursion scheme is called a catamorphism^2. Let us try to define it:

// Catamorphism draft
// WARNING: DOES NOT COMPILE
// def cata[F[_]: Functor, T, A](structure: F[T])(algebra: F[A] => A): A =
//   algebra( structure.map(cata(_)(algebra)) )
// end snippet CataWrong

// start snippet Fix
// Fixed point type
case class Fix[F[_]](unfix: F[Fix[F]])
// end snippet Fix

// start snippet CataRight
// Catamorphism
def cata[F[_]: Functor, A](structure: Fix[F])(algebra: F[A] => A): A =
  algebra(structure.unfix.map(cata(_)(algebra)))

There is one problem with this code, however. In a recursive structure, T is supposed to be of the same type as F[T] by definition. Or else we will not be able to map it by cata as above, since cata will need a Functor[T]. In other words, F[T] == T. If so, we should also be able to write structure: T instead of structure: F[T] in the signature. Obviously, we can not have that in Scala, so what do we do?

Fixed-point types

Theory. A fixed point of a function f(_) is a value x such that f(x) == x. We can think of a higher-order function fix that computes a fixed point of its argument: fix(f) == x such that f(x) == x. By extension, fix(f) == f(fix(f)) holds.

What if we bring the same ideas to the type theory? By analogy, a fixed-point type of a higher-kinded type F[_] is some type T such that F[T] == T - precisely what we need. We can also have a type Fix[F[_]], such that Fix[F] == F[Fix[F]].

Fixed-point types are interesting, because they can represent a recursive structure of any desired depth as a single type:

Fix[F] == F[Fix[F]] == F[F[Fix[F]]] == ...

Practice. I am not aware of a way you can define Fix[F[_]] so that the above equality holds - the compiler will think F[T] != T for any F and T, as far as I know.

It is possible to think of a workaround, though. In our cata definition above, we need to know that F[T] == T so that we can treat T as if it was F[T]. So in practice, we do not need to convince the compiler in that equality - a simple function T => F[T] is enough.

We can emulate the fixed-point type computation as in the theory above as follows:

// Fixed point type
case class Fix[F[_]](unfix: F[Fix[F]])

So we just wrap an F[_] in this case class. Fix[F] => F[Fix[F]] can be defined as simply fix => fix.unfix.

Catamorphism: second attempt

Now we can define the catamorphism on a fixed-point type of a structure F as follows:

// Catamorphism
def cata[F[_]: Functor, A](structure: Fix[F])(algebra: F[A] => A): A =
  algebra(structure.unfix.map(cata(_)(algebra)))

Examples using `cata`

Now we can use the new cata to define our examples:

// Nat to Int
def natToInt(n: Fix[Nat]): Int = cata[Nat, Int](n) {
  case Succ(x) => 1 + x
  case Zero    => 0
}
val nat: Fix[Nat] =
  Fix(Succ(  // 3
    Fix(Succ(  // 2
      Fix(Succ(  // 1
        Fix[Nat](Zero)  // 0
      ))
    ))
  ))
val natRes = natToInt(nat)
println(natRes)  // 3

// Sum a list of ints
def sumList(l: Fix[IntList]): Int = cata[IntList, Int](l) {
  case Cons(head, tail) => head + tail
  case Empty            => 0
}
val lst: Fix[IntList] =
  Fix(Cons(1,
    Fix(Cons(2,
      Fix(Cons(3,
        Fix[IntList](Empty)
      ))
    ))
  ))
val listRes = sumList(lst)
println(listRes)  // 6

// Evaluate an expression
def eval(e: Fix[Expr]): Int = cata[Expr, Int](e) {
  case Add (x1, x2) => x1 + x2
  case Mult(x1, x2) => x1 * x2
  case Num (x)      => x
}
val expr: Fix[Expr] =
  Fix(Add(
    Fix(Mult(
      Fix[Expr](Num(2)),
      Fix[Expr](Num(3))
    )),
    Fix[Expr](Num(3))
  ))
val exprRes = eval(expr)
println(exprRes)  // 9

First thing that catches the eye, probably, is how we need to embed every layer of the recursive structures into Fix. This is cumbersome, but fine as for the proof of concept.

Notice how all of the examples are now expressed in terms of one function - cata. We have successfully abstracted the common parts of the recursive structure collapse task.

Also, notice how we have gotten rid of the recursive calls in all of our examples. The recursion is now abstracted away in cata, so that the user does not need to deal with it directly.

Matryoshka

Catamorphisms are not the only recursion scheme out there. Many more exist. And, of course, you do not need to implement them from scratch. Matryoshka is a library that specializes on implementing recursion schemes on fixed-point types of recursive structures.

Recursion scheme mechanics

The library is centered around the notion of the fixed-point types. In the diagram above, the core type classes are marked with blue "T", and their com

panion objects - with green "O". These type classes describe what it means for an arbitrary type T to be a fixed-point type.

The Based[T] type class captures the idea that a type T must "know" the type Base[_], for which (supposedly) Base[T] == T. Supposedly, since there's nothing in Based whatsoever to suggest that equality.

Recursive - to tear structures down

Recursive[T] has a single abstract method, project, and a whole lot of methods specifying various schemes of recursion you can run on T. Our cata is among them. But obviously project is of the most interest, since it is the only abstract method and hence its implementation sheds light on what it means for a type T to be Recursive.

project can be interpreted as T => Base[T]. In the section on practical applications of the fixed-point type we already discussed that it is crucial to be able to extract the type F[T] from its fixed point representation T. If T is Recursive you can extract F[T] from T, where F is the higher-kinded type T is a fixed point of. You can specify this F via a type in the companion object of Recursive - Recursive.Aux[T, F[_]].

The fact that you can extract F[T] from T is a necessary condition for the recursion schemes defined in the Recursive[T] type class. They have one thing in common: they all tear down a recursive structure. Here is an intuition for this:

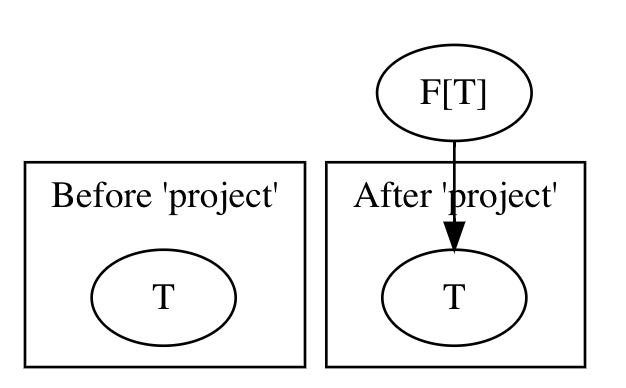
project is a "taker" - it is capable of extracting information from T. Naturally, if you take something from T, there becomes less of that something in T. This way, you can "pump" the structure, layer by layer, from T, and do whatever you want with it, until there is nothing left in T.

The arrow on the diagram points from F[T] towards T to indicate that T is a member of the structure F[T]. It does not indicate a direction of the information flow ("who takes from whom") in the project application.

Corecursive - to build structures up

It follows from the name that Corecursive is a dual of Recursive - hence, it must do the opposite thing to what Recursive does.

Indeed, it mirrors Recursive in a sense that it also has a single abstract method and a bunch of recursion schemes based on it. This method is embed and is roughly Base[T] => T. If project takes the information out of the structure and hence is good for evaluating them via algebras, embed places the information into the structure, hence building it up:

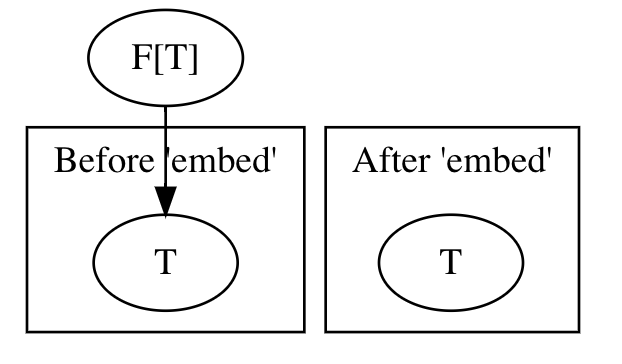
An example of a recursion scheme that takes an advantage of such a capability is anamorphism ana: (A, Coalgebra[Base, A]) => T. Coalgebra, being a dual of Algebra, is A => Base[A] and describes how to build up a single layer of the structure from A. ana aims to build deep structures using an initial element A and a way to build a single layer from it. But this is a bit out of scope of the article, since we were focusing on catamorphisms.

Examples revisited

Let us now see how to rewrite our examples from the previous chapters using Matryoshka.

First of all, make sure you apply SI-2712 fix, or else implicits won't resolve correctly and this will spoil you all the fun.

Next, do some Matryoshka imports:

import matryoshka.{ Recursive, Corecursive }
import matryoshka.data.Fix  // The fixed-point type similar to the one we implemented ad-hoc, but with Recursive and Corecursive instances.
import matryoshka.implicits._  // Syntax

And here is the code for the examples:

// Nat to Int
def natToInt[T](n: T)(implicit T: Recursive.Aux[T, Nat]): Int = n.cata[Int] {
  case Succ(x) => 1 + x
  case Zero    => 0
}
def nat[T](implicit T: Corecursive.Aux[T, Nat]): T =
  Succ(
    Succ(
      Succ(
        Zero.embed
      ).embed
    ).embed
  ).embed
val natRes = natToInt(nat[Fix[Nat]])
println(natRes)  // 3

// Sum a list of ints
def sumList[T](l: T)(implicit T: Recursive.Aux[T, IntList]): Int = l.cata[Int] {
  case Cons(head, tail) => head + tail
  case Empty            => 0
}
def lst[T](implicit T: Corecursive.Aux[T, IntList]): T =
  Cons(1,
    Cons(2,
      Cons(3,
        Empty.embed
      ).embed
    ).embed
  ).embed
val listRes = sumList(lst[Fix[IntList]])
println(listRes)  // 6

// Evaluate an expression
def eval[T](e: T)(implicit T: Recursive.Aux[T, Expr]): Int = e.cata[Int] {
  case Add (x1, x2) => x1 + x2
  case Mult(x1, x2) => x1 * x2
  case Num (x)      => x
}
def expr[T](implicit T: Corecursive.Aux[T, Expr]): T =
  Add(
    Mult(
      Num(2).embed,
      Num(3).embed
    ).embed,
    Num(3).embed
  ).embed
val exprRes = eval(expr[Fix[Expr]])
println(exprRes)  // 9

Main differences from our ad-hoc solution:

Fixed point behavior generalized: we no longer use a concrete type Fix to either build up or tear down our structures. Instead, we require corresponding behavior via Recursive and Corecursive type classes.
Nicer syntax for cata: only one type parameter and the convenient OOP-like syntax with the . - thanks to import matryoshka.implicits._.
Nicer syntax for building up the structures - previously we had to wrap every layer explicitly in Fix, now we have an embed method for it. Less parentheses.

Conclusion

Whenever you use recursion in your code, chances are that what you do is already abstracted in one of the recursion schemes. The benefit from using them instead of bare recursion is similar to the benefit when using for or while instead of goto - more concise, readable and secure code.

Matryoshka is an framework that does a great job introducing someone to these concepts. It has one rather significant drawback, however - at the moment, it is not stack-safe. For larger structures, this becomes a problem.

Nevertheless, in my opinion, every programmer aspiring to perfect their craft would benefit greatly from trying to solve their everyday recursive tasks in a more "literate" way Matryoshka offers.

Introduction to Recursion Schemes with Matryoshka

Anatolii

Recursive data structures

Natural Numbers

Lists

Expressions

Generalisation

Structure preserving transformations

New definitions for the recursive structures

Functors

Catamorphism: first attempt

Fixed-point types

Catamorphism: second attempt

Examples using `cata`

Matryoshka

Recursion scheme mechanics

Recursive - to tear structures down

Corecursive - to build structures up

Examples revisited

Conclusion

Read more

Two months of Tokyo language school

Healthy News Consumption in the Era of Web 2

Techniques to gain basic insights into ML Models

Personal Financial Projection Tool

Recursive data structures

Natural Numbers

Lists

Expressions

Generalisation

Structure preserving transformations

New definitions for the recursive structures

Functors

Catamorphism: first attempt

Fixed-point types

Catamorphism: second attempt

Examples using cata

Matryoshka

Recursion scheme mechanics

Recursive - to tear structures down

Corecursive - to build structures up

Examples revisited

Conclusion

Read more

Two months of Tokyo language school

Healthy News Consumption in the Era of Web 2

Techniques to gain basic insights into ML Models

Personal Financial Projection Tool

Examples using `cata`